Today I learned
- 시간복잡도와 공간복잡도
- 점근 표기법
- 배열과 연결리스트
- 이진탐색
- 재귀 함수
공간복잡도
공간복잡도는 입력값과 문제를 해결하는 데 차지하는 공간과의 상관관계이다
이 코드로 공간복잡도를 알아보자
def find_max_occurred_alphabet(string):
alphabet_array = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "x", "y", "z"]
max_occurrence = 0
max_alphabet = alphabet_array[0]
for alphabet in alphabet_array:
occurrence = 0
for char in string:
if char == alphabet:
occurrence += 1
if occurrence > max_occurrence:
max_alphabet = alphabet
max_occurrence = occurrence
return max_alphabet
result = find_max_occurred_alphabet
print("정답 = a 현재 풀이 값 =", result("Hello my name is sparta"))
print("정답 = a 현재 풀이 값 =", result("Sparta coding club"))
print("정답 = s 현재 풀이 값 =", result("best of best sparta"))alphabet_array = ["a", "b", "c", "d", "e", "f", "g", "h", "i", "j", "k", "l", "m", "n", "o", "p", "q", "r", "s", "t", "u", "v", "x", "y", "z"]
# -> 26 개의 공간을 사용합니다
max_occurrence = 0 # 1개의 공간을 사용합니다
max_alphabet = alphabet_array[0] # 1개의 공간을 사용합니다.
for alphabet in alphabet_array:
occurrence = 0 # 1개의 공간을 사용합니다공간을 얼마나 사용하는지는 저장하는 데이터의 양이 1개의 공간을 사용한다고 생각하자
alphabet_array의 길이 + max_occurrence + max_alphabet + occurrence으로 계산할 수 있다
26 + 1 + 1 + 1 계산하면 29만큼의 공간을 사용하는구나라고 생각할 수 있다
다음 코드도 확인해보자
def find_max_occurred_alphabet(string):
alphabet_occurrence_list = [0] * 26
for char in string:
if not char.isalpha():
continue
arr_index = ord(char) - ord('a')
alphabet_occurrence_list[arr_index] += 1
max_occurrence = 0
max_alphabet_index = 0
for index in range(len(alphabet_occurrence_list)):
alphabet_occurrence = alphabet_occurrence_list[index]
if alphabet_occurrence > max_occurrence:
max_occurrence = alphabet_occurrence
max_alphabet_index = index
return chr(max_alphabet_index + ord('a'))
result = find_max_occurred_alphabet
print("정답 = a 현재 풀이 값 =", result("Hello my name is sparta"))
print("정답 = a 현재 풀이 값 =", result("Sparta coding club"))
print("정답 = s 현재 풀이 값 =", result("best of best sparta"))alphabet_occurrence_list = [0] * 26 # -> 26 개의 공간을 사용합니다
for char in string:
if not char.isalpha():
continue
arr_index = ord(char) - ord('a') # 1개의 공간을 사용합니다
alphabet_occurrence_list[arr_index] += 1
max_occurrence = 0 # 1개의 공간을 사용합니다
max_alphabet_index = 0 # 1개의 공간을 사용합니다
for index in range(26):
alphabet_occurrence = alphabet_occurrence_list[index] # 1개의 공간을 사용합니다
if alphabet_occurrence > max_occurrence:
max_occurrence = alphabet_occurrence
max_alphabet_index = indexalphabet_array의 길이 + arr_index + max_occurrence + max_alphabet_index + alphabet_occurrence으로 계산을 한다
26 + 1 + 1 + 1 + 1로 계산을 진행하면 30만큼의 공간을 사용하는구나 라고 생각하면 된다
이 두 가지 코드를 비교하면 29의 공간을 차지하는 첫 번째 코드가 더 좋은 코드라고 생각할 수 있다
하지만 29와 30은 상수이다 시간복잡도에서 공부하면서 상수는 성능에 큰 영향을 주지 않는다 따라서 29가 더 좋은 코드라고 볼 수 없다 그렇다면 어떤 코드가 더 좋은 코드인지 알 수 있을까? 바로 공부했던 시간복잡도로 비교하는 것이다
첫 번째 코드의 시간복잡도를 알아보자
for alphabet in alphabet_array: # alphabet_array 의 길이(26)만큼 아래 연산이 실행
occurrence = 0 # 대입 연산 1번 실행
for char in string: # string 의 길이만큼 아래 연산이 실행
if char == alphabet: # 비교 연산 1번 실행
occurrence += 1 # 대입 연산 1번 실행
if occurrence > max_occurrence: # 비교 연산 1번 실행
max_alphabet = alphabet # 대입 연산 1번 실행
max_occurrence = number # 대입 연산 1번 실행alphabet_array의 길이 * 대입 연산 1번 + string길이 * 비교 연산 1번 + 대입 연산 1번 + 비교 연산 1번 + 대입 연산 2번
만큼의 시간이 필요하고 계산을 한다면
$$ 26 \times (1 + 2 \times N + 3) = 52N + 104 $$
그러면 상수를 다 제외하고 우리는 N만큼의 시간이 걸리겠구나 생각한다
두 번째 코드의 시간복잡도를 알아보자
for char in string: # string 의 길이만큼 아래 연산이 실행
if not char.isalpha(): # 비교 연산 1번 실행
continue
arr_index = ord(char) - ord('a') # 대입 연산 1번 실행
alphabet_occurrence_list[arr_index] += 1 # 대입 연산 1번 실행
max_occurrence = 0 # 대입 연산 1번 실행
max_alphabet_index = 0 # 대입 연산 1번 실행
for index in range(len(alphabet_occurrence_list)): # alphabet_array 의 길이(26)만큼 아래 연산이 실행
alphabet_occurrence = alphabet_occurrence_list[index] # 대입 연산 1번 실행
if alphabet_occurrence > max_occurrence: # 비교 연산 1번 실행
max_occurrence = alphabet_occurrence # 대입 연산 1번 실행
max_alphabet_index = index # 대입 연산 1번 실행string의 길이 * 비교 연산 1번 + 대입 연산 2번 + 대입 연산 2번 + alphabet_array길이 * 비교연산 1번 + 대입연산 3번
만큼의 시간이 필요하고 계산을 하면
$$ N \times (1 + 2) + 2 + 26 * (1 + 3) = 3N + 106 $$
상수를 다 제외하고 우리는 N만큼의 시간이 걸리겠구나 생각한다
두 코드를 비교해보자
| N의 길이 | 첫번째 | 두번째 | 비교를 위한 N^2 |
| 1 | 156 | 109 | 1 |
| 10 | 624 | 136 | 100 |
| 100 | 5304 | 406 | 10000 |
| 1000 | 52104 | 3106 | 1000000 |
| 10000 | 520104 | 30106 | 100000000 |
표를 보면 N이 아니면 성능에 그렇게 영향을 주지 못한다 따라서 공감복잡도 보다는 시간복잡도를 더 신경을 써서
코드를 작성하자
점근 표기법
알고리즘의 성능을 수학적으로 표기하는 방법이다 알고리즘의 효율성을 평가하는 방법
점근 표기법 종류는 빅오(Big-O) 표기법, 빅 오메가(Big-Ω) 표기법이 있다
빅오 표기법은 최악의 성능이 나올 때 연산량이 얼마나 걸리는지 빅오메가 표기법은 최선의 성능이 나올 때 어느 정도
연산량이 걸리는지 표기하는 것이다
다음 코드를 확인하면서 알아보자
def is_number_exist(number, array):
for arr in array:
if number == arr:
return True
return False
result = is_number_exist
print("정답 = True 현재 풀이 값 =", result(3,[3,5,6,1,2,4]))
print("정답 = True 현재 풀이 값 =", result(3,[4,5,6,1,2,3]))
print("정답 = Flase 현재 풀이 값 =", result(7,[6,6,6]))
print("정답 = True 현재 풀이 값 =", result(2,[6,9,2,7,1888]))for arr in array: # array의 길이 만큼 아래 연산이 실행
if number == arr: # 비교 연산 1번 실행
return True시간 복잡도는 N × 1로 N만큼의 시간이 걸리겠구나로 볼 수 있다
여기서 생각해보자 모든 경우가 N만큼의 시간을 꽉 채워서 걸릴까?
위 테스트에서 첫 번째 테스트를 보면 바로 결과를 찾는다 두 번째 테스트를 보면 N만큼 연산 후 결과를 찾는다
이처럼 알고리즘의 성능은 항상 동일한 게 아니라 입력값의 패턴에 따라서 달라진다
즉 첫 번째 경우가 최선의 성능으로 Ω(1) 빅오메가 표기법을 표현하고 두 번째 성능이 최악의 성능 O(N) 빅오 표기법으로 표현할 수 있다 위 테스트에서 최선의 경우는 1번이다 최선의 경우는 굉장히 적다 그리고 우리는 항상 최악의 경우를 생각해야 한다 그래서 빅오메가보다는 빅오 표기법으로 알고리즘을 분석해야 한다
배열과 연결리스트
배열은 중간에 빈방이 없어야 하는 호텔이고
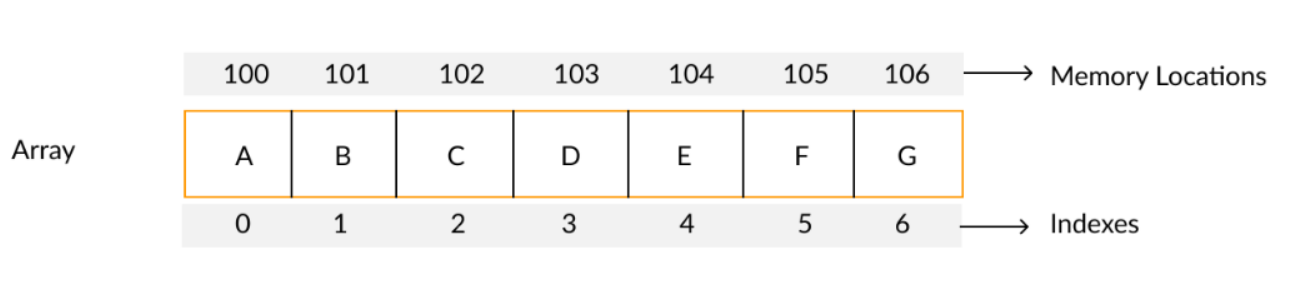
연결리스트는 입구가 하나뿐인 기차이다

배열과 연결리스트의 차이점
| 배열 | 연결리스트 | |
| 특정 원소 조회 | O(1) | O(N) |
| 중간에 삽입 삭제 | O(N) | O(1) |
| 데이터 추가 | 데이터 추가 시 모든 공간이 다 찼다면 새로운 메모리 공간을 할당 받아야한다 | 모든 공간이 다 찼어도 맨 뒤 노드만 동적으로 추가하면 된다 |
| 정리 | 데이터에 접근하는 경우가 빈번하면 배열을 사용하자 | 삽입 삭제가 빈번하다면 연결리스트를 사용하자 |
이진탐색 (Binary search)
정렬된 리스트에서 검색 범위를 줄여 나가면서 검색 값을 찾는 알고리즘
정렬된 리스트에서만 사용할 수 있는 단점이 있지만, 검색이 반복될 때마다 검색 범위가 절반으로 줄기 때문에
속도가 빠르다는 장점이 있다
동작 방삭은 배열의 최솟값과 최댓값을 더해서 2로 나눈 중간값을 구하고 그 중간값으로 검색 값을 비교한다
중간값이 검색 값이랑 같다면 바로 찾은 거고 작다면 중간값을 최솟값으로 바꾸고 크다면 중간값을 최댓값으로 바꾼다
결과를 찾을 때까지 반복한다
| 1 | 2 | 3 | 4 | 5 | 6 | 7(검색값) | 8 | 9 | |
| 1단계 | 최소값 | 중간값 | 최대값 | ||||||
| 2단계 | 최소값 | 중간값 | 최대값 |
| 1 | 2 | 3(검색값) | 4 | 5 | 6 | 7 | 8 | 9 | |
| 1단계 | 최소값 | 중간값 | 최대값 | ||||||
| 2단계 | 최소값 | 중간값 | 최대값 |
정렬된 리스트에서 이진탐색을 사용하면 시간 복잡도가 얼마나 효율적인지 알아보자
총 숫자가 1~N까지라고 한다면
1번 탐색에서 N / 2
2번째 탐색에서 N / 4 ---> N / 2^2
3번째 탐색에서 N / 8 ----> N / 2^3
k번째 탐색은 N / 2^k개가 남는다
이분탐색으로 1개가 남았다고 가정해보면 N / 2^k = 1의 수식으로 표현할 수 있다
k = log2N이라고 표현하는데 상수는 빼버리자 그러면 시간 복잡도가 O(logN)만큼 시간이 걸리겠구나 생각할 수 있다
재귀함수
함수가 자기 안에서 자신을 호출하는 함수를 재귀 함수라고 한다
아래 코드를 보면서 재귀 함수를 확인해보자
def count_down(number):
if number < 0: # 만약 숫자가 0보다 작다면, 빠져나가자!
return
print(number) # number를 출력하고
count_down(number - 1) # count_down 함수를 number - 1 인자를 주고 다시 호출한다!
count_down(60)이런 식으로 자기 자신을 계속 부르다가 특정 조건에 맞으면 리턴으로 함수를 종료한다
조건이 없으면 무한루프에 빠지니까 조심하자
'과거공부모음' 카테고리의 다른 글
| 나의 개발일지 TIL(Today I learned) - 알고리즘 자료구조 특강 및 복습 (1) | 2022.11.24 |
|---|---|
| 나의 개발일지 TIL(Today I learned) - 알고리즘 특강 및 복습 (0) | 2022.11.23 |
| 나의 개발일지 TIL(Today I learned) - 파이썬, 자바스크립트, 자료구조와 알고리즘 (1) | 2022.11.21 |
| 나의 개발일지 WIL(Weekly I learned) - 미니프로젝트 (0) | 2022.11.20 |
| 나의 개발일지 TIL(Today I learned) - 미니프로젝트 5일차 (0) | 2022.11.18 |